Классическая теория структуры силового поля инерции и гравитации

Излагается теория, фактически являющаяся математическим и физическим раскрытием эмпирического закона гравитации И.Ньютона. Она полностью соответствует принципам пространственно-временной симметрии. В рамках теории определена структура единого силового поля инерции и гравитации, полностью состоящая из квантов механической энергии гравитонов. Определено волновое полевое уравнение для расчета потенциалов. Решение уравнения выявило структуру в каждой свободной точке Пространства в виде дифференциальной системы из двух встречных продольных сферических волн. Размещение в этой точке материального тела вызывает реакцию структуры с образованием вокруг тела собственного субпространства в форме сходящейся продольной сферической волны. Её реальное существование является бесспорным свидетельством наличия внутренней замкнутости Вселенной.

В современной научной физике нет инвариантной теории гравитации, эмпирически заложенной ещё И.Ньютоном, но математически ещё никем не раскрытой. Первой попыткой на этом пути было введение С.Пуассоном понятия потенциального поля гравитации и полевого уравнения для определения его структуры. Гравитационное поле считалось статическим, а источником его принималась произвольно распределенная в пространстве масса материальных тел. Уравнение Пуассона имеет вид:

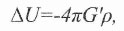                      (1)

где ∆-дивергентный оператор Лапласа,

U-потенциал гравитационного поля,

G'-гравитационная постоянная,

ρ-произвольно распределенная плотность вещества.

Выдвигаемая теория показывает, что ни то ни другое из этих былых утверждений, положенных в основу уравнения, не соответствуют действительноти. Однако это полевое уравнение Пуассона вместе с общеизвестной формулой Всемирного Тяготения долгое время считалось общепринятой теорией гравитации Ньютона. Однако эта теория оказалась ещё и не инвариантной относительно поворота во времени. Это потребовало от неё отказаться и в замен продолжить поиски новой и свободной от отмеченных здесь дефектов.

Выдвигаемая теория от них свободна. Она содержит адекватное математическое раскрытие физических механизмов инерции и гравитации в рамках единого стационарного силового поля механической природы. И делается это путем предварительного определения его структуры из гравитонов.

При этом массы материальных тел в качестве источника этого поля в теории не фигурируют, вопреки общепринятому заблуждению на этот счет.

Cиловое поле инерции и гравитации (ИГп), как единый их источник, принимается тождественным Пространству Вселенной, подразумевая и тождество их физических свойств. В виду имеется однородность, изотропия и фундаментальная стационарность структуры этой упругой среды.

В качестве безальтернативной обменной частицы в ИГп принимается гипотетическая пока энергетическая частица-квант гравитон. Он отнесен как, например, и фотон к группе калибровочных бозонов. Эти частицы обладают световой скоростью и соответствующим импульсом при отсутствии у них массы покоя. В силовом ИГп гравитоны обладают свойством быть присоединенными (адсорбированными, связанными) материальным телом в количестве, пропорциональном его массе, в процессах с приобретением им механической энергии. В обратных процессах с высвобождением этой энергии высвобождаются и гравитоны в той же пропорции. Более фундаментальным свойством по созданию самого силового ИГп материальные тела не обладают, вопреки общепринятому заблуждению.

Сила инерции возникает в ИГп в динамических процессах при использовании сторонней силы для разгона материального тела. Инерция здесь может быть определена, исходя из третьего закона механики о силовом взаимодействии двух материальных объектов. Речь идет о материальном теле и ИГп.

Упомянутые силы там равны по величине и противоположны по направлению. Сторонняя через посредство материального тела приложена к материальному ИГп, а противонаправленная инерционная – к материальному телу.

И такое проявление инерции по отношению к точечному материальному объекту должно обеспечиваться структурой ИГп в любой координатной точке пространства и любой момент времени под действием сторонней силы произвольной величины и направленности.

Это требование из житейского опыта идет в разрез с общепринятой гипотезой о природе сил инерции, якобы обязанных своим происхождением всему материальному наполнению Вселенной. Эта концепция принадлежит Э.Маху, её же придерживался и А.Эйнштейн. Но, как представляется, такое могло бы быть реально существующим только в случае однородного и изотропного распределения этого наполнения в пространстве. Однако по факту мы такого никак не наблюдаем.

А отсюда могут быть сделаны и соответствующие логические выводы о характере структуры ИГп, способной выполнить поставленное требование.

Означенное выше требование к структуре ИГп по логике сводится к необходимости следующего. Вокруг каждой точки Пространства всегда должен находиться соответствующий набор силовых агентов поля (гравитонов), способных осуществить адекватную инерционную реакцию. Набор должен быть сферой из окружающих точку гравитонов. Их вектора напряженности (силовые) и направления распространения, должны быть сходящимися в этой точке. Во времени это должен быть сходящийся в точке сферический поток гравитонов. Точнее это сходящаяся продольная сферическая волна, если учесть дуальную корпускулярно волновую природу гравитона. Естественным же продолжением сходящегося в точке потока (волны) является поток (волна) из неё расходящаяся.

Сама рассматриваемая точка оказывается одновременно «стоком» для волны сходящейся и «истоком» для волны расходящейся. С позиций математической физики это две условно независимые, равные по интенсивности (производительности) и противоположные по знаку (направлению), совмещенные точечные сферические дивергенции поля, обозначаемые как Div G₁ и -Div G₁.

Для продольной сферической волны, возбуждаемой точечным источником в однородной и изотропной упругой среде ИГп, потенциал U(ρ,t) зависит только от времени t и расстояния ρ от центра волны.

Полевое уравнение для потенциала расходящейся волны от условного точечного источника с положительной дивергенцией Div G₁ в этом случае принимает следующий вид [ 1 ]:

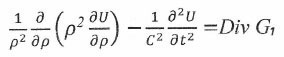                      (2)

Первый член этого неоднородного волнового уравнения, является всё тот же дивергентный оператор Лапласа. Он представлен в сферической системе координат, как наиболее практичной в изотропном пространстве. Второй член фактически обусловлен наличием волнообразного движения гравитонов в поле с постоянной световой скоростью С в стационарном режиме.

Сходящаяся волна, если представить её в обратно текущем времени, подобна волне расходящейся. Различие в замене на противоположные знаков у ρ и t параметров в функции распределения потенциала U(ρ,t).

Иными словами и для отрицательной дивергенции – Div G₂ может быть использованным то же самое полевое уравнение. Требуется лишь указанное изменение в нем имеющихся знаков у параметров. Тогда для сходящейся волны получается аналогичное уравнение, но с другой соответствующей правой частью:

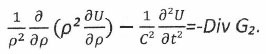                      (3)

В нем используется обратный ход времени и обратное направление волны.

В итоге потенциал для объединенного поля может быть найден путем решения следующего суммарного однородного волнового уравнения с нулевой правой частью.

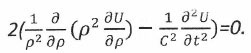                      (4)

Очевидно, что решение здесь должно состоять из двух подобных друг другу частей, различающихся знаками у параметров.

Известное в литературе [1] решение этого уравнения действительно имеет две именно такие составляющие в форме сферических волн противоположных направленностей, т.е. расходящейся и сходящейся с общим центром в рассматриваемой точке ИГп:

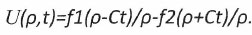                      (5)

Это же выражение для потенциалов ИГп удается получить непосредственно, исходя из свойства его фундаментальной стационарности в любой точке пространства.

Для начала следует уточнить определения для основных характеристик ИГп, представляющих его структуру. Имеются в виду потенциал U(ρ,t) и напряженность поля G(ρ,t),в сферической системе координат с центром в рассматриваемой точке пространства. В этих функциях параметр ρ в отличие от t является нелинейным в криволинейной сферической системе координат, что необходимо учитывать в последующем при их дифференцировании и определени производных.

Потенциалом ИГп в системе единиц СИ называется величина, численно равная работе A[Дж], совершаемой полем по перемещению материального тела единичной массы m[кг]из данной точки на бесконечность, т.е.U(ρ,t)[Дж/кг]= A/m. В эквивалентной формулировке потенциалом поля в данной точке является величина, численно равная значению потенциальной энергии точечного объекта единичной массы, размещенного в этой точке.

Вектор напряженности в точке ИГп является отношением величины силы F[H],действующей там на точечную массу m[кг], к величине этой массы, т.е. G[H/кг]=F/m.

Стационарность ИГп заключается в том, что напряженность поля и потенциал там остаются неизменными во времени во всей области их определения. Иначе говоря, они постоянны в каждой конкретной точке Пространства. Следовательно для них должны быть справедливыми следующие выражения:

для любого промежутка времени.

Но при наличии их зависимости от двух аргументов одновременно, это осуществимо только если между переменными имеется пропорциональная зависимость вида ρ=Сt. Константа С имеет здесь размерность скорости распространения рассматриваемых элементов структуры вдоль координаты ρ. Это cкорость гравитонов и одновременно фазовая скорость волн потенциала и напряженности поля. Иначе говоря, требуемое здесь условие пропорциональности имеется в ИГп.

Наличие (6) и(7) дает право приравнять к нулю дифференциалы указанных там постоянных функций, но с учетом их нелинейного характера. Для корректного выполнения операций дифференцирования и определения производных необходима известная линеаризация этих функций:

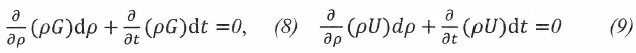
Они так же действительны во всей области определения аргументов ρ и t.

Из условия C=ρ/t=const следует и соотношение dp/dt=C, что приводит к

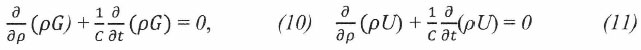
Далее используется условие зависимости вектора G от потенциала U через градиент последнего. В условиях сферической системы координат величина вектора (модуль) принимает вид следующего скалярного выражения:

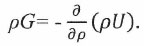                      (12)

При подстановке (12) в выражение (10) последнее переходит в:

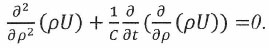                      (13)

В свою очередь (11) может быть преобразовано к виду:

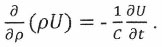                      (14)

После подстановки (14) в (13) получается уравнение для потенциала в известной форме однородного волнового уравнения Д’Аламбера:

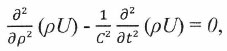                      (15)

записанного в линейной системе координат для линейной же функции ρU.

Небольшое преобразование (15) приводит его к виду:

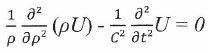                      (15')

т.е. того же самого уравнения, но записанного уже в сферической системе координат для нелинейной функции потенциала U(ρ,t).

Левые части этих уравнений являются выражениями для дивергентного оператора Лапласиана в указанной системе координат. В сферической этот оператор может быть представлен в трех эквивалентных формах:

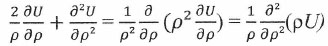                      (16)

Уравнение (15) может быть использовано для определения линейной функции ρU(ρ,t), а затем и самого потенциала U(ρ,t).

Его общеизвестное решение, получаемое методом Д’Аламбера, имеет вид:

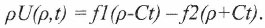                      (17)

Из (17) выражение для потенциала приобретает форму:

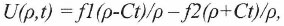                      (18)

в точности совпадающую с представленной ранее в (5).

Здесь как и в (5) ƒ1 и ƒ2-произвольные функции обозначенных аргументов, не исключая и констант.

Полученное решение применимо к любой точке ИГп не содержащей его источников, т.е. к любой точке Пространства. Иначе говоря, в каждой точке свободного от материальных тел Пространства структура ИГп представляет собой дифференциальную (уравновешенную) суперпозицию двух встречных волн продольного сферического типа. По типу это сходящаяся и расходящаяся волны, проходящие эту точку навстречу друг другу.

Стационарность характеристик ИГп определяет выбор вида функций ƒ1 и ƒ2, которым следует быть константами равной величины для обеспечения ранее принятого условия в (7).Сама величина констант на данном этапе рассмотрения потенциала существенного значения не имеет. Ясно, что после их подстановки в (18) становится очевидной полная взаимная компенсация слагаемых потенциала во всем Пространстве. Но в нем остается стоячая волна с нулевым потенциалом и нулевой напряженностью поля, которая ненаблюдаема, но неизменно там присутствует.

В таком состоянии ИГп является максимально упорядоченным, т.е.обладающим минимальной энтропией. Потому, как представляется, оно успешно может претендовать на статус изначального состояния Вселенной до появления в ней Вещества.

Представленное в (18) выражение для потенциала с учетом (15) показывает, что ИГп оказалось самоподдерживающимся дифференциальным полем без источников. Его встречные волны не могут существовать по отдельности. Это возможно только в такой дифференциальной системе с их взаимными переходами из одного вида в противоположный.

Так сходящаяся волна, проходящая через каждую точку ИГп, переходит в ней в состояние расходящейся. А такая в свою очередь может перейти в состояние сходящейся только на пути её распространения на бесконечность.

Если реально существует внутренняя замкнутость Пространства ( ИГп), то, пройдя её, расходящаяся волна на обратном пути уже оказывается в состоянии сходящейся. Другого механизма такого взаимного обращения одного состояния волны в противоположное вероятно не существует. А это является весомым, если не бесспорным, доказательством реального существования внутренней замкнутости Пространства Вселенной.

Обнаруженная в структуре ИГп полная взаимная компенсация встречных волн потенциала и напряженности поля в любой точке пространства совсем не эквивалентна их полному там отсутствию. Они никак себя не проявляют при отсутствии материальных объектов, размещающихся в структуре ИГп.

Однако ситуация кардинально меняется, если там находится точечный материальный объект, обладающий массой m1. Структура реагирует на это тем, что проходящая через данную точку сходящаяся волна частично «экранируется» точечной массой. Имеет место условная адсорбция (связывание) массой части гравитонов на приобретение ею потенциальной энергии, по величине пропорциональное этой массе. Это создает соответствующее ослабление на выходе волны расходящейся. Нарушается существовавший ранее баланс в пользу волны сходящейся. Одновременно в точке возникает отрицательная дивергенция, пропорциональная адсорбции, т.е. и величине m1.

Как и все прочие процессы в изотропном пространстве, эта точечная дивергенция является сферически симметричной. Математически связанный с нею потенциал сходящейся волны U1(ρ,t) вокруг точки m1 имеет форму второго слагаемого в выражении (19) и приобретает вид:

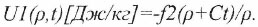                      (19')

Константа f2 в нем пропорциональна m1. Коэффициент пропорциональности должен иметь размерность гравитационной постоянной G' и именно ею и является. Таким образом стационарная величина U1,от времени уже не зависящая, в точке нормирования амплитуды волны при ρ=1 составляет:

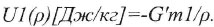                      (20)

Учитывая обратно пропорциональную зависимость потенциала и напряженности поля от ρ,принято считать их равными нулю на бесконечности. При этом условии величины потенциалов в поле сходящейся волны по их определению принимают отрицательные значения. Это так и отражено в (19)и(20).

Если теперь вторую материальную точку массы m2 разместить на расстоянии ρ первой, то в точке её размещения будет присутствовать отрицательный потенциал сходящейся волны. Он соответствует выражению (20).

Выраженная через его градиент напряженность поля приобретает вид:

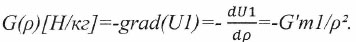                      (21)

Её вектор ориентирован по радиусу в направлении точки m1.

В результате направленная в ту же сторону сила F(ρ), воздействующая на массу m2 и ей пропорциональная, оказывается равной:

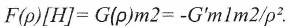                      (22)

В итоге, как и ожидалось, выражение для расчетной гравитационной силы в точности соответствует (тождественно) выражению для Закона Всемирного Тяготения И.Ньютона.

Суть инерции в механике проявляется в форме реально существующей силы инерции, возникающей в динамических процессах при движении тел с ускорением. Величина ускорения в ИГп ограничивается на уровне, определяемом напряженностью поля в месте расположения движущегося тела.

Эта величина и численно, и по размерности полностью равна этой напряженности. Именно ею величина ускорения полностью и определяется, независимо от того, движется ли рассматриваемое тело под действием сторонней силы или силы гравитационной. В обоих случаях фигурирует одна и та же масса, будь она «тяжелой» или «инерционной» по определению. Т.е. это понятия тождественные, а не эквивалентные, как ошибочно считается.

Определение характеристик инерционной реакции логическим методом на базе использования третьего закона механики было уже продемонстрировано ранее. Для математического же их определения можно использовать тот же пример динамического процесса с разгоном материального тела точечной массы m сторонней силой F. Здесь удобно воспользоваться формулой для определения потенциала U(ρ) в ИГп через работу A, затрачиваемую силой на перемещение в нем этой массы. Независимо от конкретного направления сторонней силы в связанной с телом сферической системе координат, оно всегда радиально и направлено по координате ρ в сторону от материального тела. Последнее естественно находится в центре окружающей его сходящейся сферической волны.

Потенциал в ИГп, создаваемый там по определению работой сторонней силы, является положительным и соответствующим выражению:

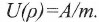                      (23)

Определение работы произведением силы на длину передвижения, дает

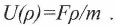                      (24)

Отношение величины сторонней силы к величине массы тела определяет его ускорение a, что приводит к соотношению:

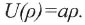                      (25)

Напряженность поля G(ρ), определяемая через градиент потенциала, есть:

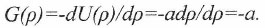                      (26)

Исчезновение в (26) зависимости от ρ показывает, что в нем фигурирует напряженность поля в точке расположения перемещаемой массы, а величина G численно равна ускорению, но вектор направлен в противоположную сторону. Соответственно, инерционная сила F', порождаемая ИГп и приложенная к массе m, определяется выражением:

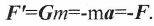                      (27)

Численно она является равной и противоположно направленной по отношению к силе сторонней.

Реальность рассчитанной таким образом инерционной силы F' ни чуть не меньшая, чем найденной подобным же образом силы гравитационной, реальность которой не подвергается сомнению, Этим же подтверждается и их единая природа.

Легко доказуемая одновременность появления обеих действующих сил в процессе ускоренного движения, делает инерционную из них, подобной некой отрицательной обратной связи. Она поддерживает стабильное ускорение в динамических процессах и стабильность скорости в статических. В последних она подавляет возможные флуктуации и фактически реализует физическое выполнение первого закона механики.

I. Единое ИГп является материально энергетическим, волновым и состоящим полностью из частиц-квантов механической энергии гравитонов. Это фактически самоподдерживающаяся полевая структура без источников.

II. Фундаментальная стационарность ИГп позволяет на её базе определить вид волнового полевого уравнения для распределения потенциала поля, которое известно как линейное волновое уравнение Д'Аламбера.

III. Найденная с его помощью структура ИГп в любой свободной его точке представляет собой дифференциальную пару из двух встречных продольных сферических волн: сходящейся в этой точке и расходящейся из неё.

IV. Самоподдерживающаяся дифференциальная система сферических волн ИГп имеет возможность для существования благодаря наличию внутренней замкнутости Пространства Вселенной.

V. Помещенное в любую точку ИГп материальное тело создает в ней эффект «возбуждения» структуры поля, с образованием сходящейся продольной сферической волны вокруг этого объекта.

VI. Эта волна образует, выделенное для материального тела, собственное субпространство (инерциальную систему отсчета), в котором и проявляются по отношению к нему инерционные, гравитационные и релятивистские воздействия (эффекты).

VII. Посредством полевого уравнения математически рассчитана величина силы гравитации между двум точечными массами в ИГп. Расчетная формула для этого в точности совпадает (тождественна) Формуле Всемирного Тяготения И.Ньютона.

VIII. Аналогичный расчет инерционной силы в динамическом процессе с материальным телом подтвердил её величину, найденную априори путем применения третьего закона механики, как и реальность её существования.

IX. Утверждается её определяющее влияние в качестве некой обратной связи на стабилизацию ускорения в динамических процессах и скорости в статических.

X. Подтверждено единство природы и тождество масс инертной и тяжелой, ранее считавшихся только эквивалентными.

XI. Выдвигаемая теория по факту является математическим и физическим раскрытием того, что называется классической теорией гравитации И.Ньютона, и одновременно расширенной в область инерции.

XII. Теория обладает всеми видами симметрии, которые обуславливают соблюдение законов сохранения для энергии, импульса, момента импульса и четности. Она инвариантна относительно преобразований вида трансляции и вращения пространства и времени, а так же и Лоренц-инвариантна.

1. Яворский Б.М., Детлаф А.А. Справочник по физике.- 4-е изд. М. 1979. Стр. 539.

©Все права зарезервированы. Коммерческое использование запрещается без письменного разрешения автора. Права пользователей регламентированы в рамках международной лицензии СС BY-NC-SA 4.0

P.S. Данная теория явилась результатом мозговой атаки, проведенной совместно с сыном Дмитрием, радиофизиком, и внуком Алексеем, к.ф.н. Несмотря на отсутствие по разным причинам этих имен в списке авторов, их соавторство остается бесспорным, о чем я здесь официально и заявляю.